为交流近年来在偏微分方程及其应用领域所取得的最新研究成果, 研讨相关的前沿课题,同时促进偏微分方程相关领域的专家,特别是青 年学者之间的交流与合作,华南理工大学数学学院和广东工业大学数学 与统计学院将于 2023 年 5 月 18 日举办《2023 年偏微分方程青年研讨会》。 会议详细信息如下:
一、 学术委员会
陈智奇 李用声 卫雪梅 朱长江 (主席)
二、 组织委员会
洪光益 彭红云 谢启林 翟小平
三、 主办单位:
广东工业大学数学与统计学院
广东工业大学数学与统计学院 (代章)
2023 年 5 月 17 日
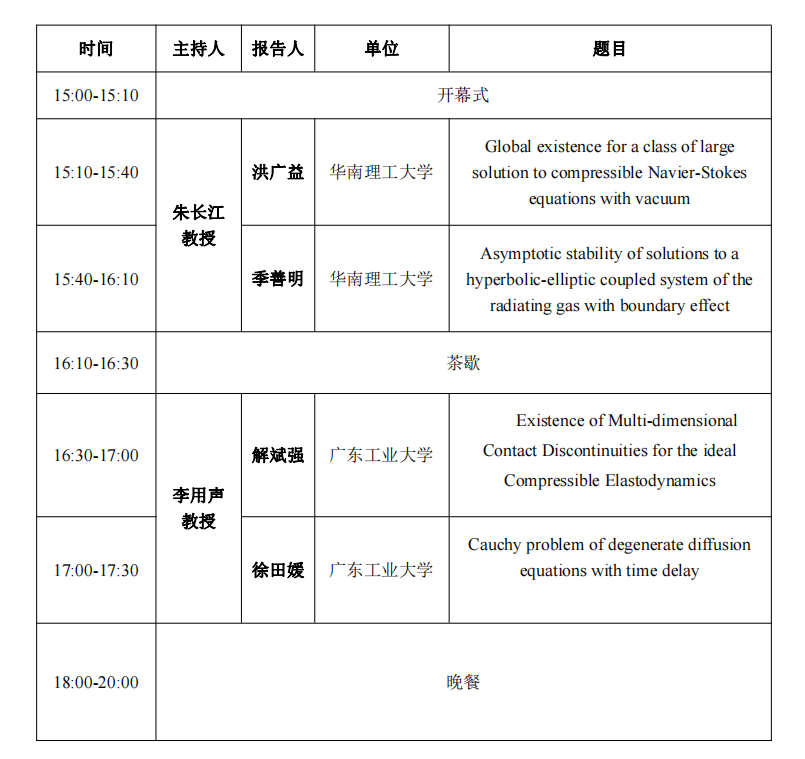
会议日程 (5 月 18 日星期四)
ABSTRACT
Global existence for a class of large solution to compressible Navier-Stokes equations with vacuum
洪广益
In this talk, we are concerned with the Cauchy problem of the three-dimensional isentropic compressible Navier-Stokes equations. We prove the global existence and uniqueness of classical solutions with large initial energy and vacuum, under the assumptions that the fluid is nearly isothermal (i.e., the adiabatic exponent $\gamma$ is sufficiently close to $1$), and that the far-field density $\tilde {\rho}$ is either vacuum or close to vacuum. To the best of our knowledge, we establish the first result on the global existence of large-energy solutions with vacuum to the three-dimensional compressible Navier-Stokes equations for the cases of vacuum and nonvacuum far-field constant states, which generalizes the result in [X.D. Huang, J. Li, Z.P. Xin, Comm. Pure Appl. Math., 2012] on classical solutions with vacuum and small energy (large oscillations). This is joint work with Xiaofeng Hou, Hongyun Peng and Prof. Changjiang Zhu.
Asymptotic stability of solutions to a hyperbolic-elliptic coupled system of the radiating gas with boundary effect
季善明
This talk is concerned with the asymptotic stability of the solution to an initial-boundary value problem with boundary effect for a hyperbolic-elliptic coupled system of the radiating gas corresponding to the rarefaction wave case and shock wave case respectively. For the scalar viscous conservation law and rarefaction wave case, it is known by Liu, Matsumura, and Nishihara (SIAM J. Math. undefined. 1998) that the solution tends toward rarefaction wave or stationary solution or superposition of these two kind of waves. Motivated by their work, we prove the stability of the above three types of wave patterns for the hyperbolic-elliptic coupled system of the radiating gas with small perturbation. A singular phase plane analysis method is introduced to show the existence and the precise asymptotic behavior of the stationary solution. The stability of rarefaction wave, stationary solution, and their superposition, is proved by applying the standard L^2-energy method. The asymptotic stability of shock wave case is also considered. This is a joint work with Minyi Zhang and Changjiang Zhu.
Existence of Multi-dimensional Contact Discontinuities for the ideal Compressible Elastodynamics
解斌强
Contact discontinuities are most typical interfacial waves for systems of hyperbolic conservations.We prove the existence of the multi-dimensional compressible elastodynamic contact discontinuities in both 2D and 3D in Sobolev spaces without any additional constraints which remove the stability condition in {Guiqiang Chen, Paolo Secchi and Tao Wang, Stability of Multidimensional Thermoelastic Contact Discontinuities, Arch. Rational Mech. undefined. 237 (2020) 1271– 1323}. The key ingredients of our analysis are Lagrangian coordinates, the transversality of the deformation tensor, and an viscous approximation. This talk is based on a joint work with Jiaxu Li(CUHK).
Cauchy problem of degenerate diffusion equations with time delay
徐田媛
This talk is about propagation speed of degenerate diffusion equations with time delay. We show the asymptotic spreading speed and its coincidence with the critical wave speed of sharp wave, and prove that the initial perturbation or the boundary of the compact support of the solution propagates at the critical wave speed for the time-delayed degenerate diffusion equations. Different from the existing studies related to spreading speeds, the time delay makes the critical speed of traveling waves slow down in a more complicated fashion such that the critical speed cannot be determined by the characteristic equation, and the degenerate diffusion causes the loss of regularity for the solutions. By a phase transform technique we construct upper and lower solutions with semi-compact supports and then we determine the asymptotic spreading speed.