报告题目：Existence of at most two limit cycles for some non-autonomous differential equations

报告人：赵育林教授（中山大学数学学院（珠海））

报告时间：2022年11月18日 14：30—15：30

报告地点：677552363 （腾讯会议）

主持人：乔守红

报告摘要：It is know that the non-autonomous differential equations  dx/dt=a(t)+b(t)|x|, where  a(t)  and b(t) are 1-periodic maps of class 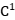, have no upper bound for their number of limit cycles (isolated solutions satisfying  x(0)=x(1)). We prove that if either  a(t) or  b(t) does not change sign, then their maximum number of limit cycles is two, taking into account their multiplicities, and that this upper bound is sharp. We also study all possible configurations of limit cycles. Our result is similar to other ones known for Abel type periodic differential equations although the proofs are quite different.

报告人简介：赵育林，中山大学数学学院（珠海）教授、博士生导师。研究方向为向量场分支理论、常微分方程及其应用。近几年来，赵育林教授一直从事向量场分支理论和周期单调性的研究工作，已在J. Differential Equation、Nonlinearity、中国科学(英文版)等杂志发表文章七十余篇(包括与别人合作的文章)。先后主持国家自然科学基金6项、教育部留学回国人员启动基金一项。 2007年入选教育部新世纪优秀人才支持计划，获2019年度广东省自然科学奖二等奖。